很多期权初学者在使用单一期权作方向型预测时，经常苦恼于“为什么我的方向预测对了，可是期权交易还是亏损？”。

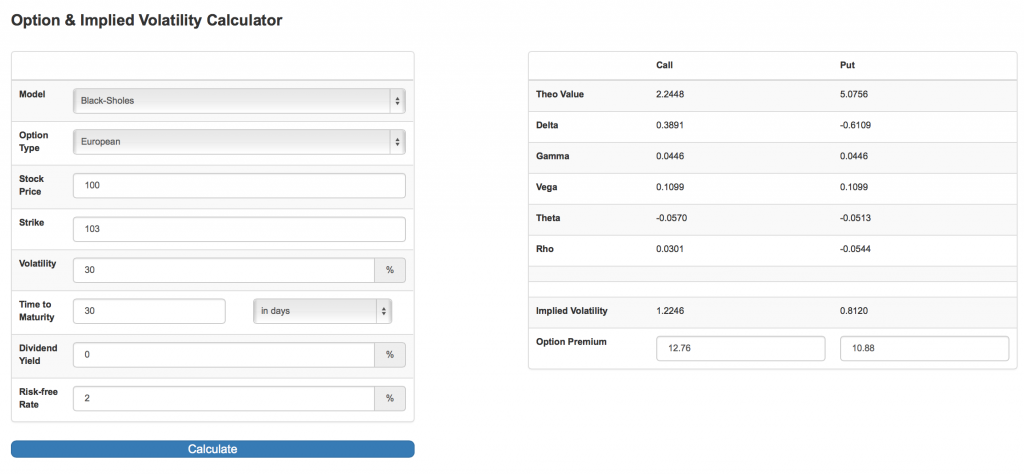
例如投资者买入一个月到期看涨期权：

• 当前股票价格：100
• 距到期日时间：30天
• 行权价：103
• 隐含波动率：30%

将上述参数输入到期权计算器，我们可以得出看涨期权价格为2.24。

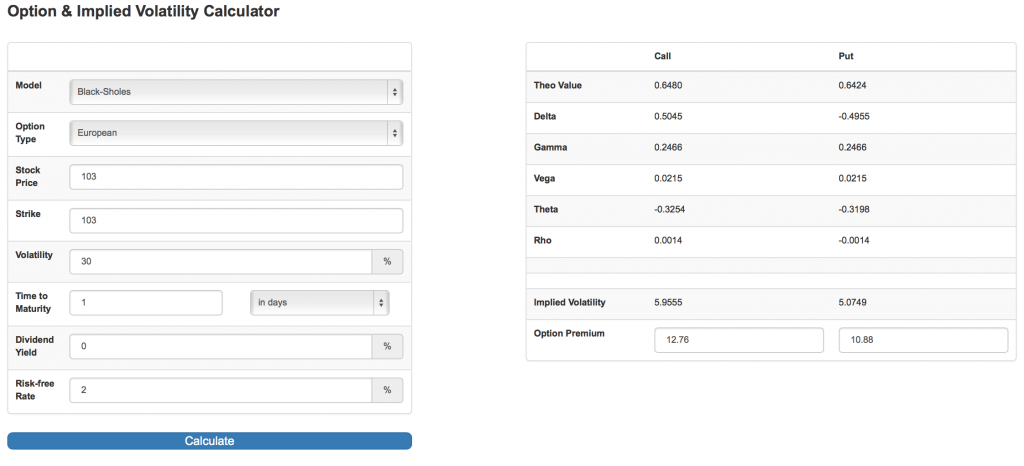
假设股票价格的确如投资者预期，在到期日前上升到103，此时我们重新计算期权价格：

• 股票价格：103
• 行权价：103
• 距到期日时间：1天 (通常期权到期日为周六，最后交易日为周五，仍有一天有效期)
• 波动率：30%

虽然股票价格上涨到投资者预测的103，但此时期权价格却下降为0.65，交易账面损失1.65；如果接下来到周六有效期截止时，市场没有出现任何重大利好消息，则期权到期作废，期权价值为零，交易损失100%。

读者很容易可以得出到期日损益平衡点的股票价格为：105.24。这意味着只有在到期日股票价格超出105.24时，交易才有可能盈利。

上面的例子揭示了投资者在单一利用期权杠杆功能做市场方向型投机时，需要更大的股票价格波动，才能盈利。

那么为什么方向预测正确，投资反而亏损呢？

我们之前的基础知识中曾经介绍，期权的价值由内在价值和时间价值两部分组成。内在价值，对于看涨期权来说，是股票价格超出行权价的数量，也就是期权的实值部分；时间价值是期权有效期内股票价格有可能超出行权价的概率价值。对于上面例子中的虚值看涨期权，期权的价值等于期权的时间价值。

既然时间价值依赖于股票价格超出行权价的概率，那么直觉告诉我们：

• 距期权到期日时间越长，概率越高，时间价值越大
• 股票波动率越高，概率越高，时间价值越大
• 股票价格离行权价越近，概率越高，时间价值越大

显然，当到期日临近，如果股票价格没有超出行权价，时间价值将逐渐衰减为零。

上面的论述揭示了期权交易中的一个重要属性：时间损耗或时间衰减。希腊字母中的Theta就是专门用来描述期权的时间损耗速度的。

Theta的理论定义

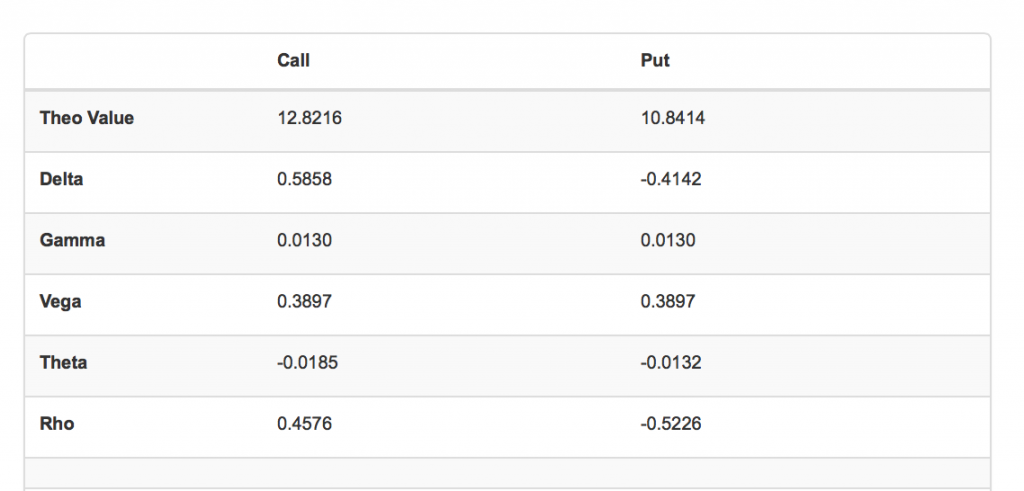
Theta在理论上定义为期权价值因为时间推移而下降的速度。现实中我们可以用Theta值大概估计在其它变量恒定前提下，一天时间期权价值的损失量。例如下面是期权计算器默认页面中的Theta值。

如上图所示，看涨期权Theta为-0.0185，这代表如果其它变量恒定，一天之后，期权价格将由现在的12.8216，下降为12.8031。事实上，如果我们在计算器中修改到期日时间为364天，重新计算后期权价格为12.8030，验证了我们用Theta进行的推算。

对于一个合约单位为100的期权，0.0185的Theta意味着每个合约在一天中会损失1.85。

在期权交易中，我们通常将Theta称为Theta账单，对于大多数期权来讲，买入方每天都要像支付房租一样支付Theta账单，来保留合约的权利。

Theta的特性

Theta的特性比较繁多复杂，我们列举几个基本特性。

(在下面的讨论中，我们以Theta的绝对值来比较Theta的大小)

• 通常买入期权Theta值为负

对于大多数期权，Theta在多数情况下为负值，意味着买入方每天支付Theta账单。

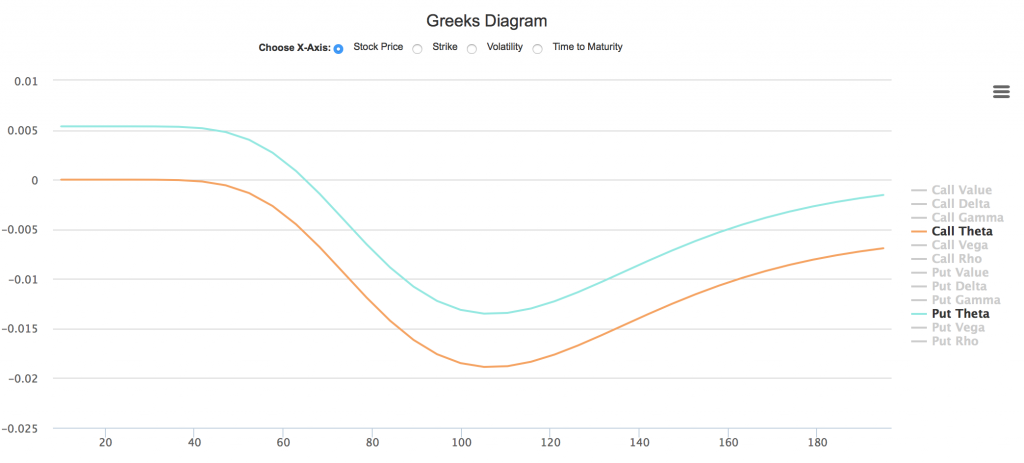
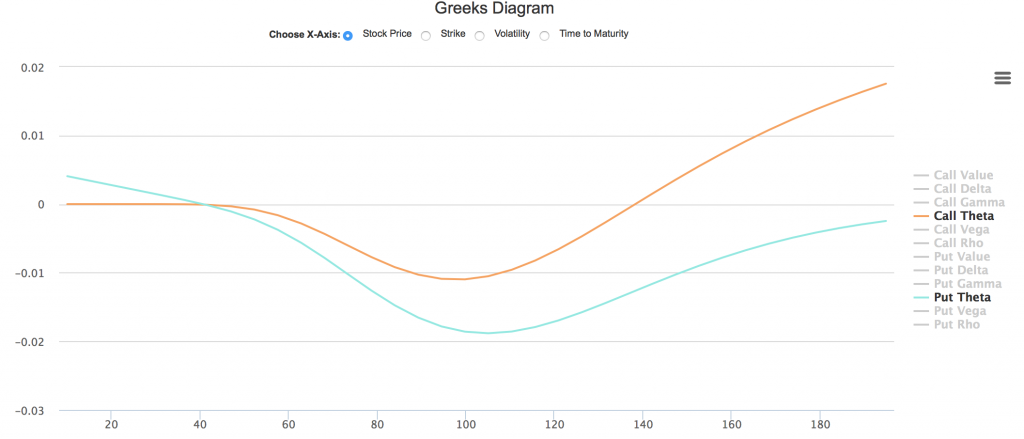
读者可以在我们的期权计算器页面的希腊字母动态图中，选择看涨、看跌期权Theta作为显示内容，横坐标选择股票价格。

如上图所示，只有深度实值看跌期权(S<60, K=100)，Theta值会成为正值，也就是投资者买入深度看跌期权，可能逐日收取Theta账单。其中原因与无风险利率有关，我们这里不作详细探讨。

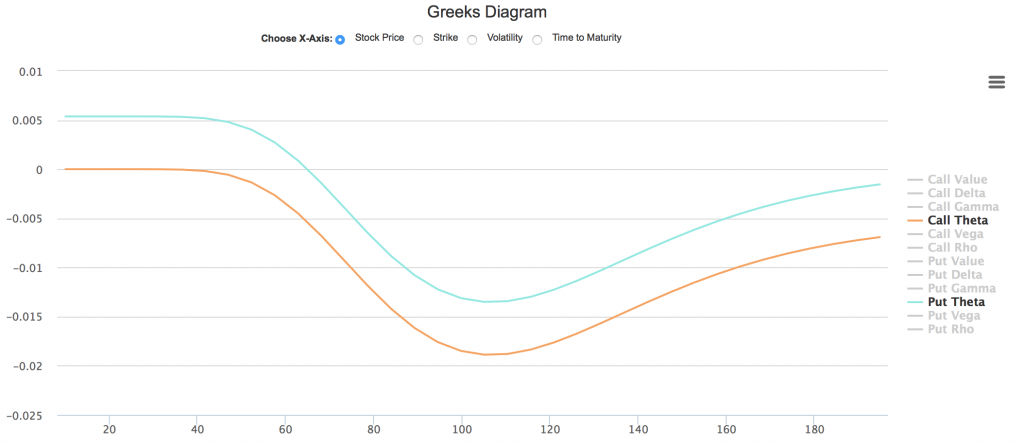
此外，当标的股票派息时，实值看涨期权的Theta也有可能成为正值。例如，我们将期权计算器中股息率修改为5%，可以得到下图：

图中可以看出，当股票价格超过140，看涨期权(黄色)为深度实值，此时Theta为正。

• 平值附近，Theta值最大

如果其它因素相同，那么平值附近的期权Theta值最大，也就是说平值期权的时间损耗最高。相同显示的是Theta相对于股票价格。可以看出，Theta在实值附近(100 - 110)达到峰值。

下图将横坐标选为行权价，同样我们可以看到实值附近Theta达到峰值。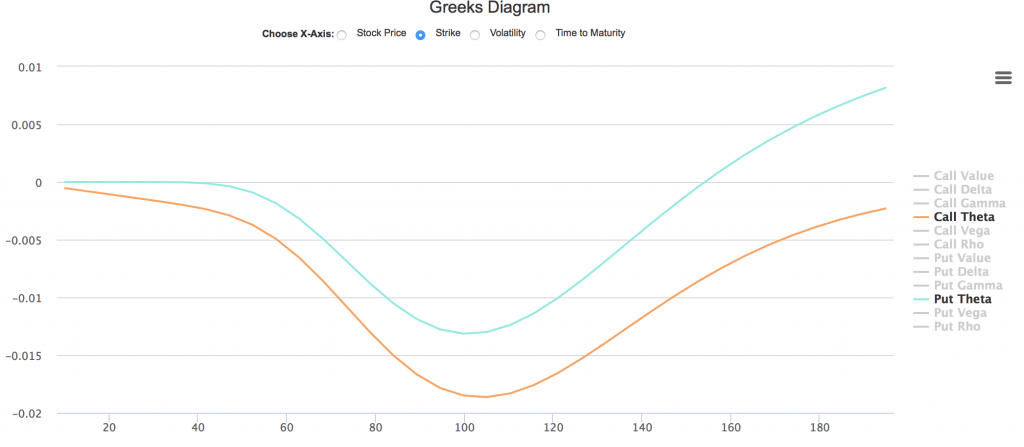

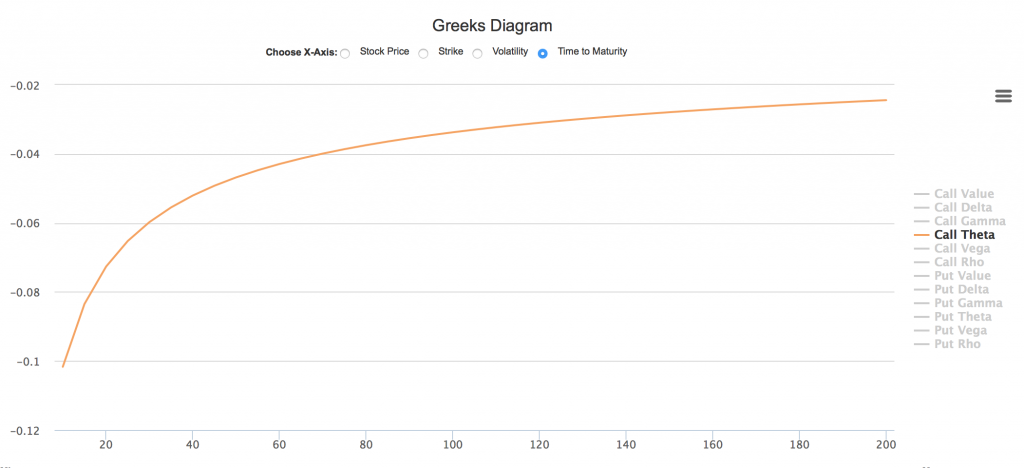
• 平值期权，随到期日临近，Theta快速飙升

在Theta定义一节中，举例的Theta比较小(到期日365天，Theta=-0.0185)，但如果我们修改到期日为10天，我们会发现Theta上升为-0.1017，即每个合约一天损失10.17。

当我们将到期日修改为2天时，我们看到Theta继续飙升到-0.2242，即每个合约一天损失22.42。

我们用希腊字母动态图可以更清晰的显示这个特性：

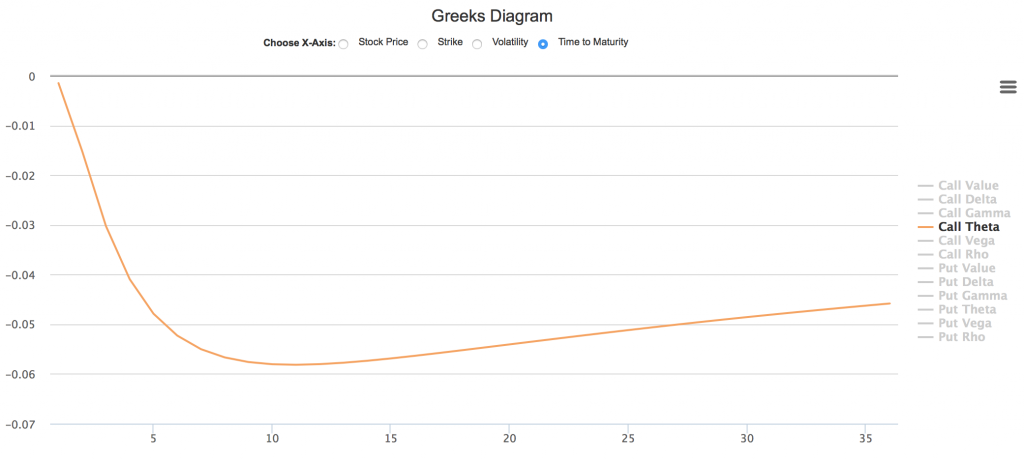
读者注意上面分析适用于平值期权。对于虚值和实值期权，Theta经常表现比较复杂，但通常在到期日前呈下降趋势。例如下图展示轻度虚值(股票价格95)看涨期权Theta随时间先上升后下降的特性。

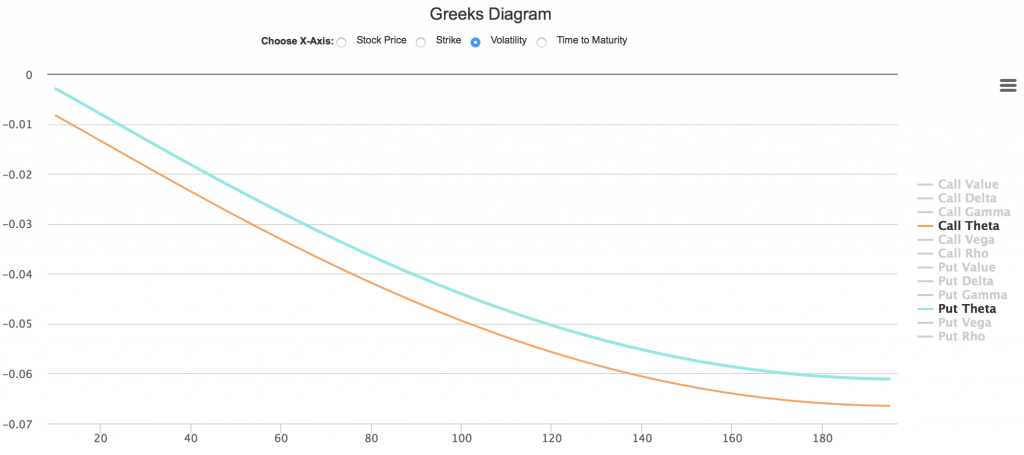
• Theta随波动率增加而增加

除了受股票价格，时间，股息等因素影响外，Theta对波动率的变化也非常敏感。如下图所示，将横坐标选择为波动率：

可以看出，随着波动率增加，Theta(绝对值)增加。

Theta的实用意义

在很多交易中，无论我们处于期权买方还是卖方，我们都要严格监测Theta的当前数值，以及其它市场因素变化，可能为Theta带来的影响。下面我们以两个之前文章介绍的实战交易策略举例。

• 备兑开仓(Covered Call)策略中Theta的作用

在备兑开仓策略解析一文中，我们解释了该策略的交易动机之一是依赖于期权的时间损耗来获取盈利，而时间损耗就是我们这一节讲解的Theta。

在明白了Theta的特性之后，读者就可以部分解答文中的一个挑战问题：

如何寻找适合的看涨期权？

我们上面的学习中了解了以下两个有关特性：

－ 平值附近期权Theta最高

－ 期权在到期日临近时，Theta大幅增加

这两个特性是我们合理构建备兑开仓策略的关键因素之一。显然，在其它市场变量相同情况下，选择短期、平值或轻度虚值的看涨期权，可以为我们带来最佳的时间损耗收益。实际操作中，在确定好交易标的和交易时机后，投资者通常选择卖出一个月左右到期的轻度虚值看涨期权。

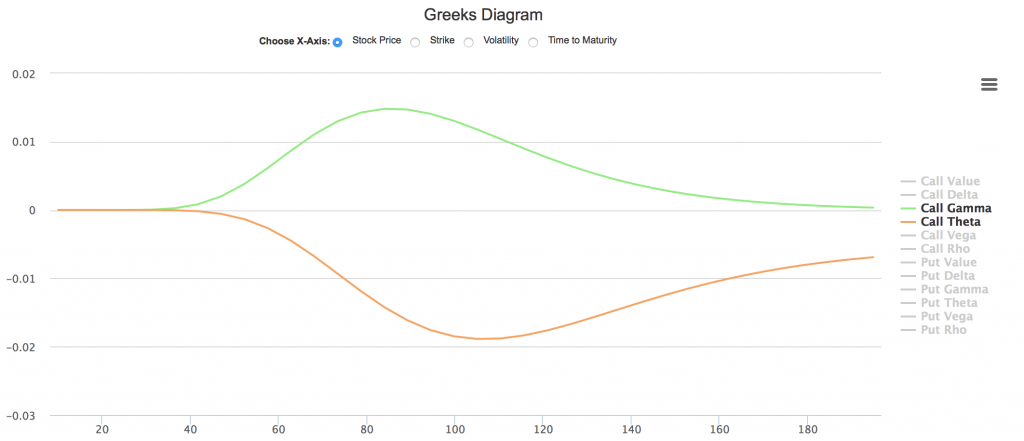
• Gamma交易中，如何合理匹配Theta与Gamma

在Gamma是你的朋友一文中，我们提到Gamma和Theta是一对形影不离的孪生兄弟。他们互相制约，此消彼长。

例如，我们在动态图中同时选择看涨期权的Gamma和Theta作为显示内容：

显然，Gamma总是为正，Theta总是为负；Gamma较高的区域，Theta也相对较高。这张图就清晰解释了我们在Gamma交易中遇到的困境 －当市场波动，投资者从Gamma多头中获得盈利时，需要支付Theta账单。只有在Gamma盈利大于Theta账单时，整体交易才可能盈利。

既然我们明白了这一对互相制约的因子的内在机制，我们就可以合理选择标的股票及期权组合，选择Gamma/Theta比例较高的期权，以扩大Gamma盈利，减少Theta支出。