上篇帖子中，我们为读者讲解了作为期权风险系数的希腊字母中的第一个字母Delta。

读者还记得Delta是期权价格相对于标的股票价格变化的敏感度。期权的Delta不是固定不变的，会随标的股票价格、波动率、股息率、和无风险利率等其它变量变化而变化。而在期权风险系数中描述Delta相对于标的股票价格变化的敏感度，就是我们这一节的主题：Gamma。

Gamma的定义

Gamma的理论定义为期权的Delta相对于标的股票价格的变化率。通俗来讲，在其它变量恒定前提下，当股票价格发生微小变化时，期权Delta的变化量就是Gamma。

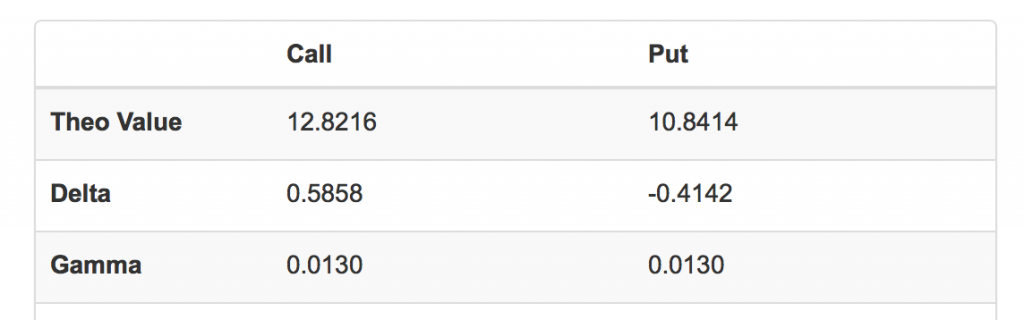
举例来说，在期权计算器默认页面，我们得到如下结果：

以看涨期权为例，此时：Delta＝0.5858，Gamma＝0.0130，这意味着如果股票价格上涨$1，看涨期权Delta将变为0.5858＋0.0130 ＝ 0.5988。

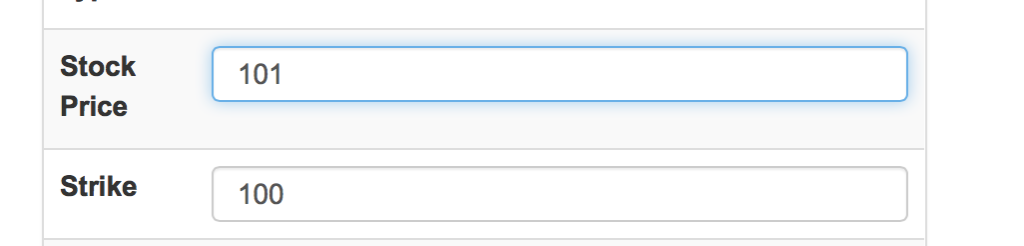
我们用计算器继续进行验证，将股票价格从100调整为101：

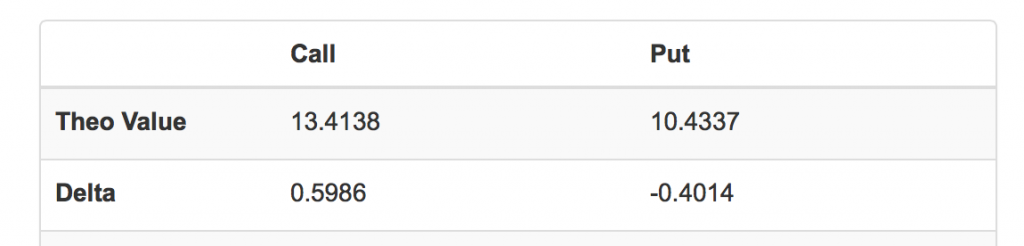
重新计算后，我们得到：

股票价格变化后，看涨期权Delta变为0.5986，和我们预期的0.5988非常接近。

如果我们进一步研究，就会发现Delta随股票价格的变化并不是线性的。事实上，准确来讲Gamma描述的是Delta变化的曲率。

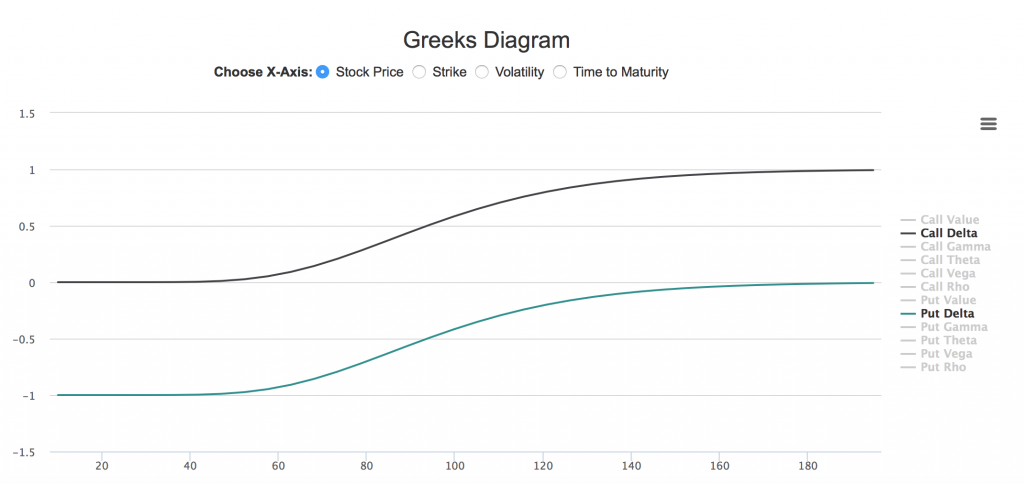
我们下面偷用一个以后会详细介绍的高级工具－希腊字母动态图－来从视觉上直观了解一下Delta和Gamma的关系。读者可以打开期权计算器，在页面默认状态下，将页面上移，读者可以看到在计算器基本输出、输入模块下，有一个图形显示区，这就是期权初学者可以充分了解期权动态特性的希腊字母动态图。

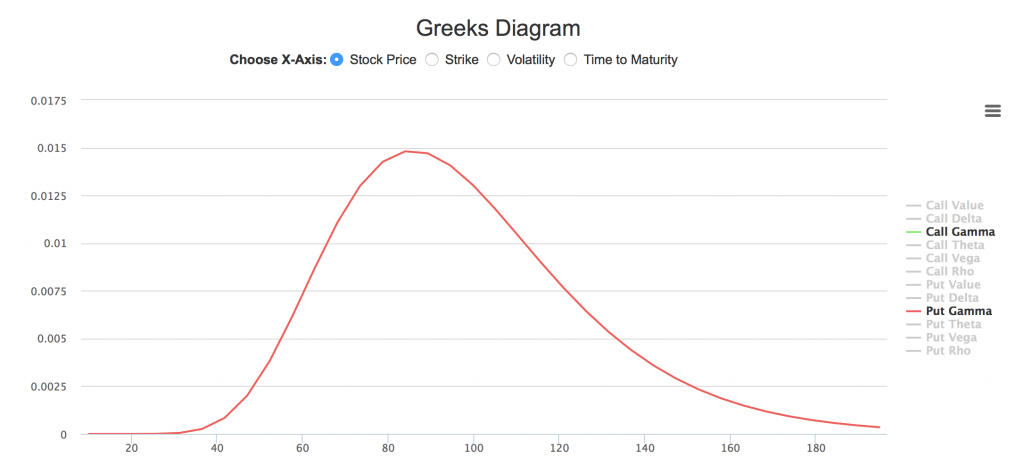
如上图所示，横坐标选择的是股票价格(从20以下到180以上)，纵坐标显示的是看涨、看跌期权Delta值。图中可以看到，看涨、看跌期权Delta随股票价格的变化是两条平行的上行曲线，看涨期权Delta位于(0, 1)之间，看跌期权Delta位于(-1, 0)之间。除去深度实值和深度虚值(股票价格远远偏离平值100)部分比较平坦外，曲线基本为凹型向凸型转换，意味着Delta的变化由缓慢逐渐加快，达到峰值后，又逐渐减缓。Delta的这种变化速度用下面的Gamma图显示就更清晰了。(读者只需在图右侧取消Delta选项，选择Gamma即可)。

显然，Gamma在股票价格极低和极高(深度虚值和深度实值)时趋近于零，在接近平值附近时迅速飙升，达到峰值后又迅速回落。这和上面的视觉观察是一致的。(Gamma的具体峰值和很多变量有关，包括距到期日时间，这里暂不作详细论述)。

那么在现实中，Delta变化的快与慢，Gamma值的高与低，有什么实际意义呢？我们尝试从Delta作为对冲比率这一内涵来解释：

• Delta作为对冲比率

从上面定义中我们知道，在股票价格变化相同情况下，Gamma高的期权Delta变化大且快，Gamma低的期权Delta变化小且慢。

当投资者用标的股票对期权策略进行Delta对冲而实现市场中性时，投资者需要随时关注股票价格变化。当股票价格变化稍大，原来的组合就会偏离中性状态，投资者需要及时买入或卖出适量的股票，使组合恢复中性，避免股票价格带来的市场风险。在连续市场(价格连续，时间连续)，这样的动态Delta对冲操作还是可行的；但在真实市场中，价格经常表现为跳跃式的波动，尤其在闭市后重新开市，价格经常出现大幅跳开，此时组合会因为偏离中性而带来策略设计中所未期待的损益。

为预警或避免这种情况的出现，交易员在监测组合的净Delta值时，还需要监测组合的净Gamma值。Gamma值高(正或者负)，意味着在相同的股票价格变化下，组合更多的偏离市场中性状态，也就是面临更多的价格风险。

Gamma的特性

同Delta一样，Gamma也会随股票价格、距到期日时间等因素变化而变化。在以后的希腊字母动态特性专题中，我们会更加详细的探讨Gamma的变化规律。以下简要介绍几个特性。读者可以在期权计算器中，自己加强练习。

• 买入期权，Gamma为正；卖出期权，Gamma为负

对于同质(相同标的、相同到期日、相同行权价)的看涨、看跌期权，Gamma值是相同的。由上面的Gamma图我们看到，买入期权时，Gamma永远为正；反之，当卖出期权时，Gamma则为负值。这一点很重要，它意味着当我们买入期权时，不论看涨还是看跌期权，我们均获得Gamma多头，当股票价格上涨时，Delta上涨；当我们卖出期权时，我们获得Gamma空头，当股票价格上涨时，Delta下降。

• 平值附近期权Gamma较高

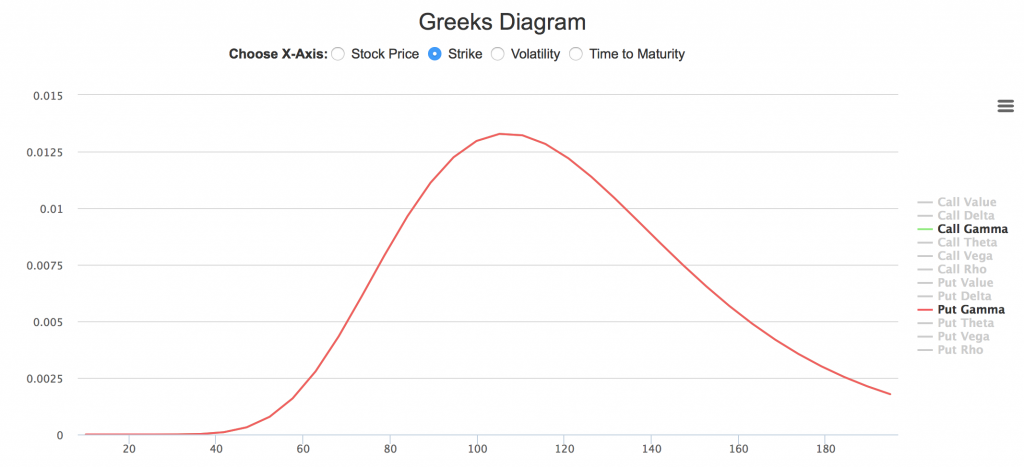
通常来讲，平值附近期权的Gamma较实值或虚值期权高。如下图所示，横坐标为行权价，标的股票价格为100；Gamma峰值出现在105左右。

• 波动率上升，Gamma下降

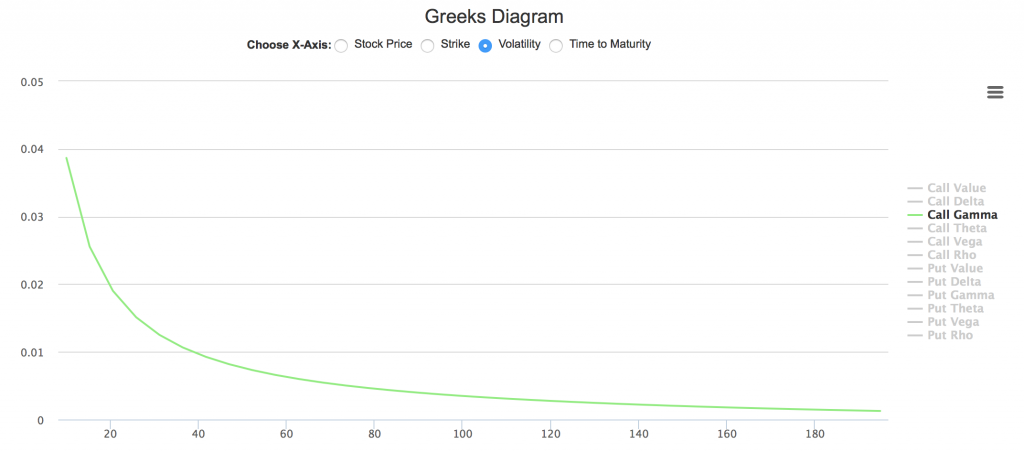
如下图所示。横坐标选取为波动率。

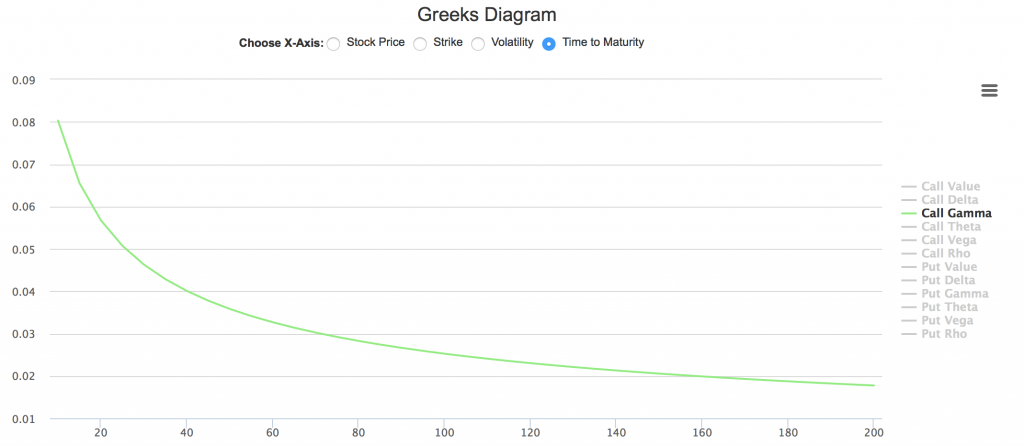
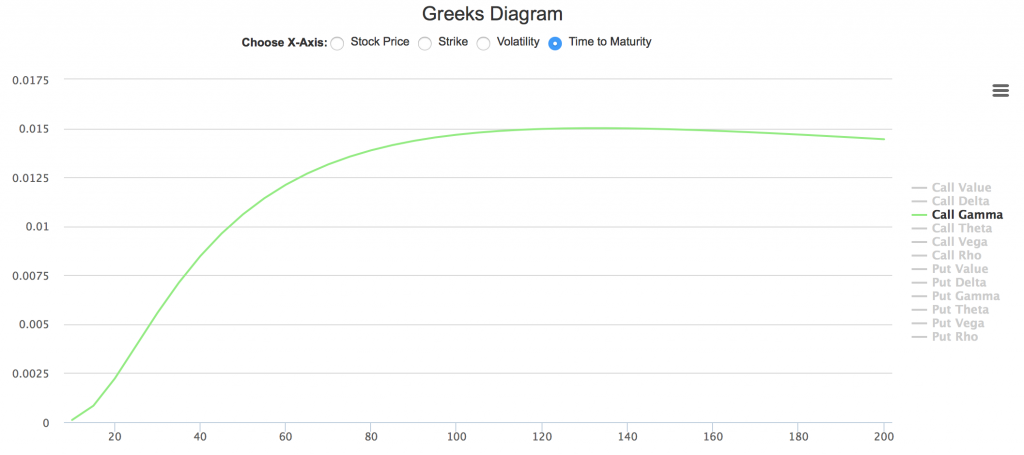
• 平值期权在到期日临近时，Gamma飙升

如下图所示，横坐标选取距到期日时间，左侧为到期日。

读者要注意，上面的特性只适合平值附近的期权，对于深度实值和深度虚值期权则恰恰相反。例如下图显示的是行权价为120的虚值看涨期权，临近到期日时Gamma迅速衰减。

Gamma是你的朋友

上面基本特性中，我们讲到买入期权，Gamma为正，获得Gamma多头。

正的Gamma代表股票价格上升时，Delta上升；股票价格下降时，Delta下降。如果我们将Delta看作我们以期权组合代替标的股票的比率，上面的描述可以重新归纳为：当股票价格上升时，我们持仓股票数量增加；当股票价格下降时，我们持仓股票数量减少。这看上去是一个非常不错的交易方式！

我们回顾本节最开始的例子：当股票价格由100变为101时，看涨期权的Delta由0.5868变为0.5986，也就是如果我们持有一个看涨合约，以相应的股票计算，我们的持仓由58.68股上升为59.86股，增加了1.2股。相反，如果股票价格有100下降为99，Delta将由0.5868下降为0.5727，即相应的股票持仓下降为57.27股，减少了1.4股。

显然，当股票价格上升，股票持仓自动增加，而当股票价格下降，股票持仓自动减少，这正是投资者理想的投资模式。现实中，的确有很多专业期权交易员和机构，利用低成本的交易优势，通过这种方法获利。在专业期权交易中，这种方法称为Gamma交易(Gamma Scalping)。下面我们通过实例帮助读者理解。

假设我们构建一个如下的市场中性策略，以期权计算器默认值为例：

• 买入一个平值看涨期权，价格12.82，支付现金12.82 x 100 = 1282; Delta为0.5858
• 同时卖出58.58股标的股票，收入现金100 x 58.58 ＝ 5858

当股票价格变动，我们根据期权Delta的变化进行动态Delta对冲：

• 当股票价格上升为101时，期权Delta为0.5986，需要重新卖出1.28股以实现市场中性。收入现金：101 x 1.28 ＝ 129.28。
• 当股票价格下降回100时，期权Delta返回0.5858，需要买入1.28股；付出现金：100 x 1.28 = 128。
• 当股票价格继续下降至99时，期权Delta为0.5727，需要买入1.31股以实现市场中性。付出现金：99 x 1.31 = 129.69。
• 当股票价格上升回100时，期权Delta返回0.5858，需要卖出1.31股；收入现金：100 x 1.31 = 131。

在上面四次的对冲交易中，我们的操作实际都是低买高卖；因此为我们带来了129.28 － 128 － 129.69 ＋ 131 ＝ 2.59的利润。

上面的例子告诉我们，当我们同时拥有Gamma多头和市场中性组合时，不论股票价格上涨还是下跌，在动态Delta对冲操作中，实现了标的股票的低买高卖，从而为组合带来盈利。细心的读者在反复练习中可以发现，Gamma交易中盈利的大小和Gamma值是正相关的。因此深入了解Gamma的动态特性，为期权初学者研究最佳交易机会，又提供了一个有效的训练领域。

与Gamma多头相反，当投资者卖出期权时(看涨或看跌)时，Gamma为负值，交易者获得Gamma空头。此时，依照上面同样操作，不论股票价格上涨还是下跌，交易都会带来亏损。

至此，读者可能会设想：如果我们都买入期权获得Gamma多头，再利用股票实现Delta对冲，那么我们不是就可以获得无风险的稳定盈利了么？但是常识又告诉我们天下没有免费午餐，那么上面的Gamma交易风险究竟在哪里呢？

其实在众多的期权风险系数当中，Gamma还有一个形影不离的孪生兄弟，那就是描述期权时间损耗的Theta。 从基础知识中，我们知道期权的价值是内在价值和时间价值的总和。在其它变量恒定前提下，随着时间推移，期权的时间价值逐渐衰退，直到到期日时，衰退为零。当投资者买入期权后，实际上是在每天支付Theta账单。现在我们就明白了上面Gamma交易中，投资者还面临Theta风险。

下一节关于Theta的解释中，我们会详细探讨Theta的特性，以及如何合理配置Gamma与Theta，从而在Gamma交易中获得交易优势。