“九章”光学实验解读（上）九章到底要解决怎样一个数学问题？

作者：徐令予

作为开场白，请允许我先提一个问题：有谁知道 Torontonian 是一个什么样的数学问题？

我的朋友圈中不少是数学和理论物理的专业人士，他们对上述问题都是一头雾水。这一点也不奇怪，即使请出谷歌和牛津英语大词典，它们的回答照样是答非所问、不知所云。牛津词典对 Torontonian 的释义是：A native or inhabitant of the Canadian city of Toronto.（加拿大城市多伦多的原住民）。

牛津词典的释义虽然没有直接给出问题的答案，但是却引出了一条线索，此事确实与加拿大的多伦多市有关。位于该市的Xanadu研究机构在2018年底发表了一篇论文，论文把使用阈值检测器进行高斯玻色采样时得到的输出分布概率定义为矩阵的一种函数，并命名它为 Torontonian（多伦多人）函数[1]。

请注意了：

• Torontonian函数绝不是一个古老的数学问题，它产生于2018年的年底；
• Torontonian函数是为某种特殊高斯玻色釆样获取量子优势而特意定制的；
• Torontonian函数并不能解决什么实际问题。

中科大的“九章”实验装置恰恰就是那种特殊的高斯玻色釆样，“九章”光学实验不是玻色釆样(BS)，也不是高斯玻色釆样(GBS)，而是“使用阈值检测器的高斯玻色采样”，又被“九章”论文审稿人亚伦森教授戏称为“Chinese Gausi-Boson Sampling"，或者叫“中式高斯玻色采样实验”。

BS、GBS 和“九章”釆样事实上都是光量子蒙特卡洛模拟过程。它们反复地让相同数量的光子一批又一批地通过一个复杂光路，然后在出口处通过光子检测得到光子分布的样本数，最后用“实验得到的频率”去等效于某种“数学计算出的概率”[2]。

虽然以上几种实验方案都属于“玻色釆样”大家族，但它们之间却有着很大的差异。这就像小汽车、皮卡和载重货车虽然都是汽车，但是它们的结构不同，当然用途也完全不一样。下面这张表格展示了玻色采样、高斯玻色釆样和“九章”高斯玻色釆样的主要区别。

这三种实验由于釆用不同的技术方案，它们面向完全不同的任务。玻色采样和高斯玻色釆样针对的数学问题分别是“积和式”(Perm)和“Hafnian”(Haf)。这两个矩阵函数均出现在 BS 和 GBS 之前，它们都与一些现实问题有关。换言之， BS 和 GBS 是企图要解决客观存在的数学问题，当然是否能够有效地解决这些问题又另当别论了。

但是“九章”实验却反其道而行之，它不是要解决一个已经存在的有实际意义的数学问题，而是把自身定义为一个数学问题，然后要求经典计算机在这个特定问题上与自己比高低。这就像一个业余射手挑战专业射手，业余射手朝墙上先射一箭，然后以箭头为中心画几个同心圆圈给专业射手当作靶子。

为什么“九章”实验装置与“积和式”及 Hafnian 计算绝缘，主要原因在于在出口处使用的是阈值检测器。也就是说，“九章”的检测端只能辩别每个出口有无光子，但没有能力辨别每个出口处究竟出现了几个光子。

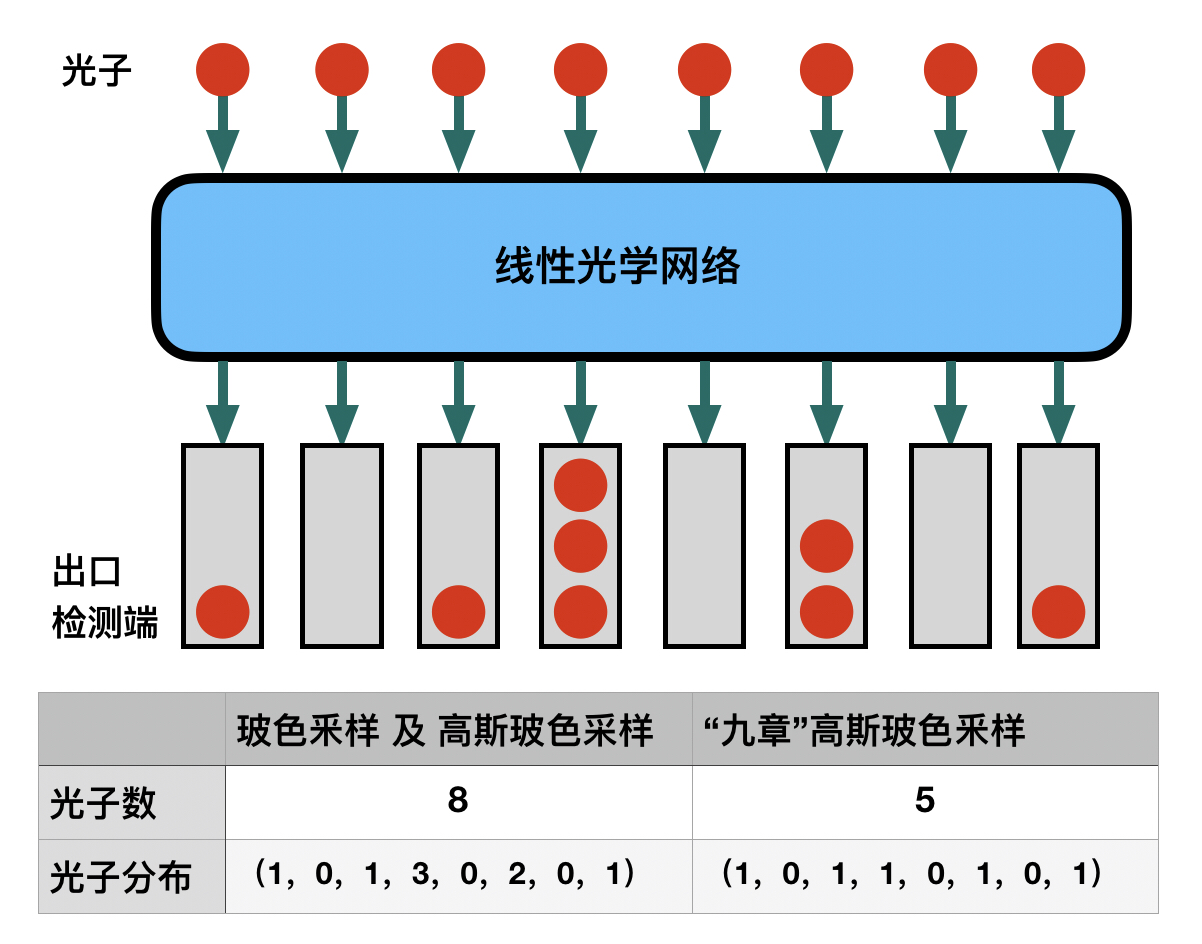
对照上图，如果第4出口处的一个光子落入了第三个出口处，对于BS和GBS得到的分布变成了（1，0，2，2，0，2，0，1）但是“九章”得到的分布不变，依然是（1，0，1，1，0，1，0，1）。“九章”无法分辨结果明显不同的两次釆样，它把两种不同的光子分布混在了一起。换言之，相较于BS和GBS，“九章”采样忽略了许多细节，结果是丢失了极有价值的信息，因此矩阵的Torontonian函数没有什么实用价值，它为“量子优势”而生，也注定为“量子优势”而死。

“九章”为什么要使用阈值检测器呢？通常被解释成：阈值检测器比光子计数器成本低、易于在市场上採购、工作条件不太苛刻。所以又有人把“九章”这类GBS称为穷人的高斯玻色釆样，它是GBS的偷工减料版，由GBS的结果可以推出“九章”的结果，但反之不然，因为九章的釆样过程中损失了许多极有价值的信息。

当然中科大团队绝对不差钱，他们在“九章”上使用阈值检测器肯定不只是为了省钱，这背后可能另有原因。玻色釆样的光源是单光子，理论上不存在争议；到高斯玻色采样改成了激光压缩态，其实就是技术上的缩水版；然后“九章”再退一步，在检测端动了手脚，把以前的“光子计数器”改为只能检测光子有无的“阈值检测器”。玻色釆样——>高斯玻色釆样——>“九章”釆样，要从这条技术路线图上认定“进化”真的很困难，但是要说“内卷”也不够正确，可能用“转进”二字最为合适。

上世纪四十年代后期，国民党的军队节节失利，攻不能胜、败又不甘，这“转进”二字道尽了当时国民党政府的凄凉和无奈，这又何尝不是今日投身于“量子优势”研究团队的心态呢。

其实“量子优势”本是个伪课题。量子计算机的理论基础至今没有得到科学家的广泛认可，四十年多年过去了，量子计算机在实际应用上是一筹莫展。如果量子计算机真能解决一个经典计算机对之朿手无策的数学问题，这不全结了，用洪荒之力搞“量子优势”毫无必要。科学家要能打硬仗把精力集中到解决实际问题上，不应去追求“量子优势”这些虚名上，否则与流量明星热衷于走穴和选秀又有何区别？

“量子优势”的炒作其实就是量子计算遭受严重挫折的真实写照，如果有一天量子计算机真的破解了1024位的RSA公钥密码算法，全世界的“量子优势”研究团队都要失业回家卖红薯。所以从另一个角度来看，如果“量子优势”炒得火热，恰恰证明量子计算在可预见的将来难有什么作为，公钥密码非常安全，量子通信工程不仅不具可行性，而且也根本没有必要性。

总之，“九章”光学实验装置不是数学问题的解决者，而是数学问题的产生者。这个新产生的 Torontonian 函数只是用来与经典计算机比高低，它并没有什么实际的应用价值。经过这般煞费苦心的安排，“九章”真能击败经典计算机取得量子优势吗？“机关算尽太聪明，反误了卿卿声名！”欲知详情 且看下文分解。

[1] Gaussian Boson Sampling using threshold detectors

（可以证明，如果在GBS过程中在同一出口处有两个或多个光子的概率足够小，即使釆用阈值检测器（仅检测光子有无），该模型也仍然很难用经典计算机进行模拟。）

[2] 人人可以懂量子科学(３)：“九章”到底解决了一个什么问题？